작업 스케줄링 문제
작업 스케줄링 문제는 작업의 수행 시간이 중복되지 않도록 모든 작업을 가장 적은 기계의 수에 배정하는 문제이다.
작업 스케줄링 문제에 주어진 문제 요소들은 작업의 수, 각 작업의 시작시간과 종료시간이다. 시작과 종료 시간이 정해져 있다는 것은 작업의 길이가 주어진 것이라고 봐도 무방하다.
그렇다면 이것들을 그리디 알고리즘으로 표현한다면 다음과 같이 표현할 수 있다.
- 빠른 시작시간 작업을 우선(Earliest start time first) 배정
- 빠른 종료시간 작업을 우선(Earliest finish time first) 배정
- 짧은 작업 우선(Shortest job first) 배정
- 긴 작업을 우선(Longest job first) 배정
하지만 첫 번째 알고리즘을 제외하고 나머지 세 가지는 항상 최적해를 찾지 못다.
알고리즘
JobScheduling
입력: n개의 작업 t1, t2, ... , tn
출력: 각 기계에 배정된 작업 순서
시작시간의 오름차순으로 정렬한 작업 리스트를 L이라고 한다.
while (L ≠ ∅) {
L에서 가장 이른 시작시간을 가진 작업 ti를 가져온다.
if (ti를 수행할 기계가 있으면)
ti를 수행할 수 있는 기계에 배정한다.
else
새로운 기계에 ti를 배정한다.
ti를 L에서 제거한다.
}
return 각 기계에 배정된 작업 순서
EX)
[s,f]에서 s는 시작시간, f는 종료시간.
t1 = [7,8],
t2 = [3,7],
t3 = [1,5],
t4 = [5,9],
t5 = [0,2],
t6 = [6,8],
t7 = [1,6]
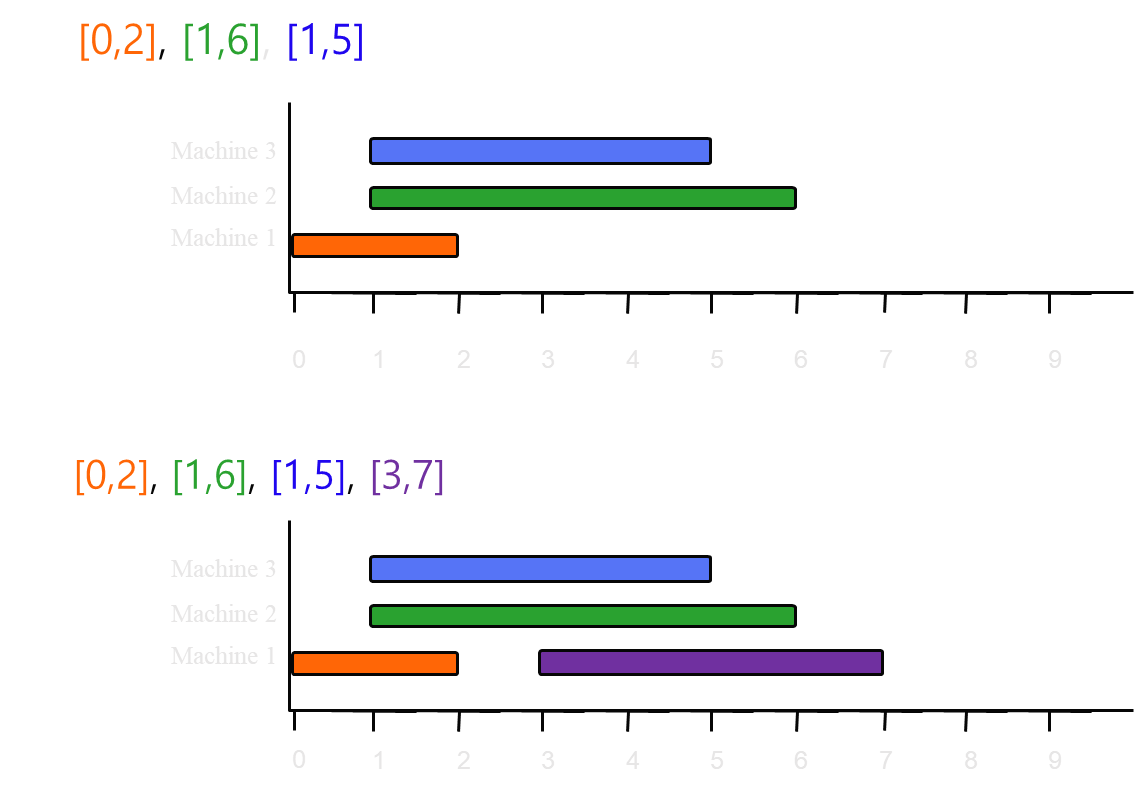
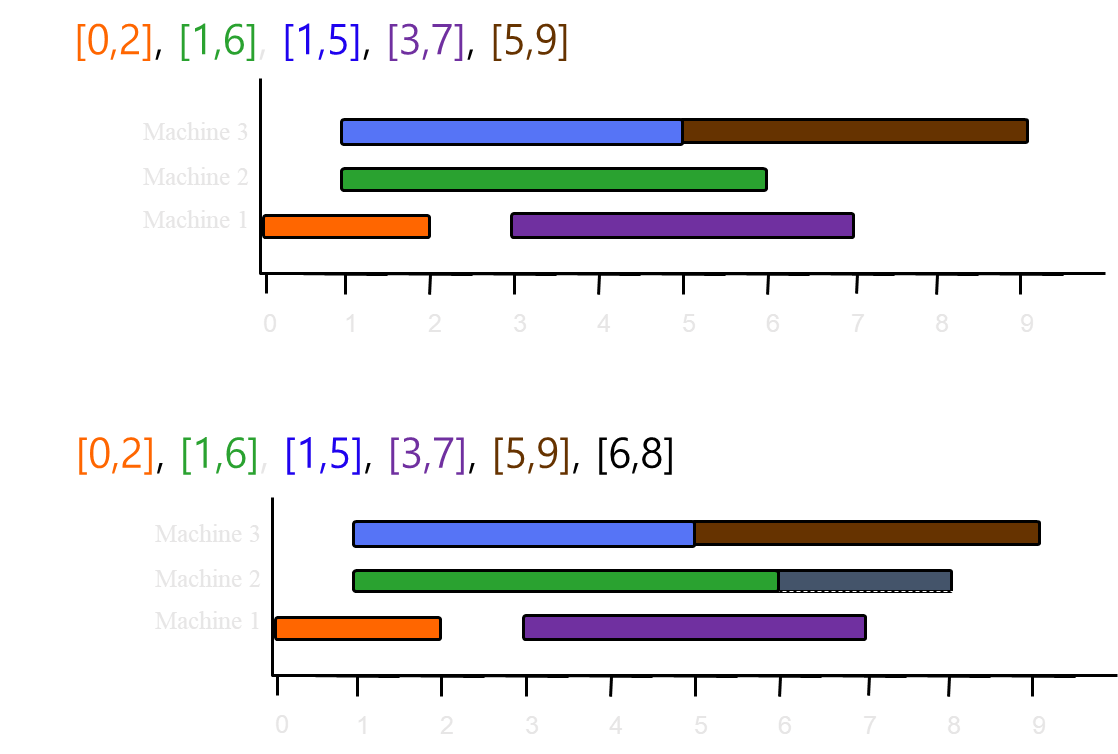
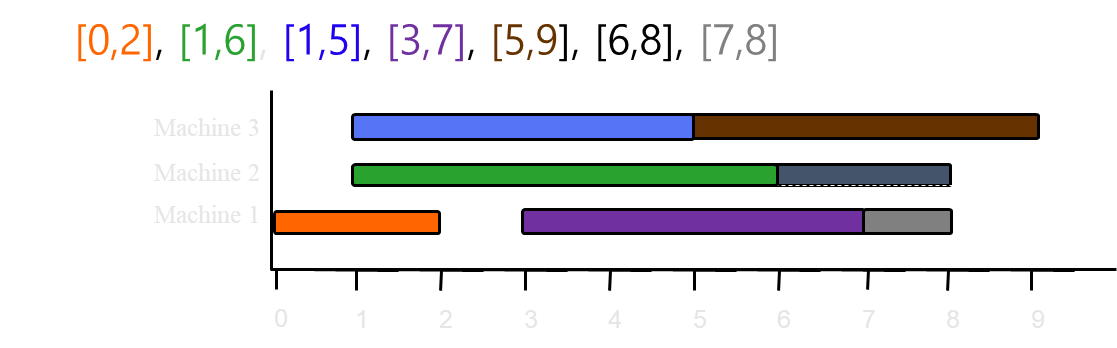
- Line 4 : L = {[0,2], [1,6], [1,5], [3,7], [5,9], [6,8], [7,8]}이다.
- Line 5~11 : while-루프를 반복 수행하면서 각 작업이 적절한 기계에 배정된다.
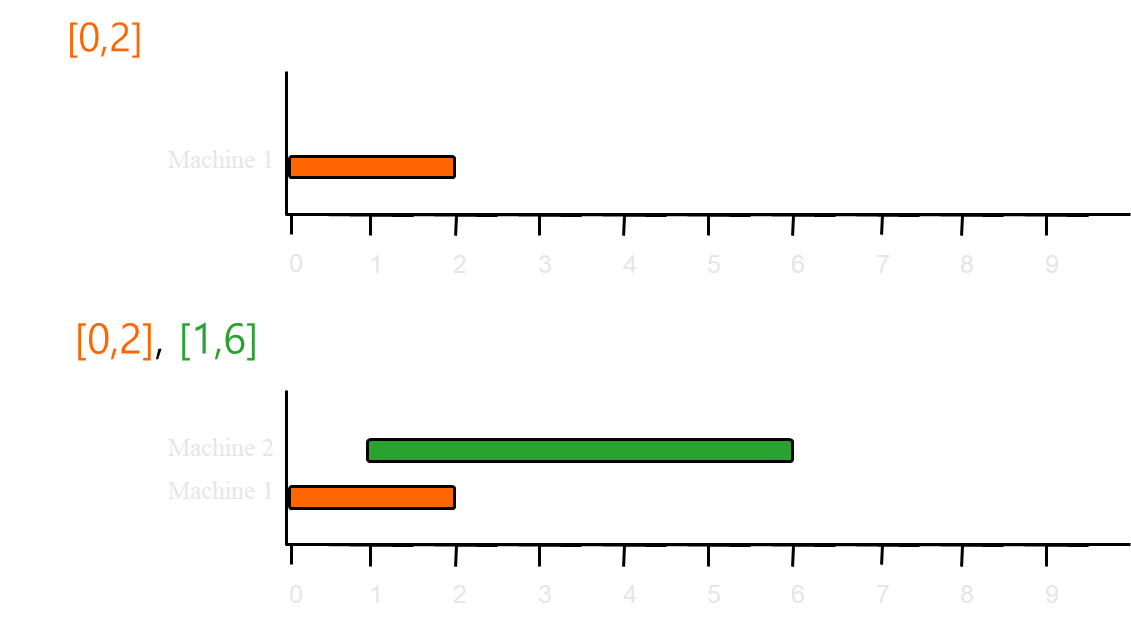
시간 복잡도
n개의 작업을 정렬 : O(nlogn)
while-루프 : O(m)(m은 사용된 기계의 수)
-> 작업을 L에 가져가다가 수행 가능한 기계 배정
while-루프가 수행된 총 횟수 : n번
JobScheduling 알고리즘의 시간복잡도 : O(nlogn) + O(m)*n = O(nlogn) + O(nm)
비즈니스 프로세싱, 공장 생산 공정, 강의실 or 세미나 룸 배정, 컴퓨터 태스크 스케줄링 등에 응용할 수 있다.
'Algorithms' 카테고리의 다른 글
| 그리디 알고리즘 - A009_HuffmanCode (0) | 2021.12.01 |
|---|---|
| 그리디 알고리즘 - 집합 커버 문제 (0) | 2021.12.01 |
| 백트래킹 기법 (0) | 2021.11.29 |
| 그리디 알고리즘 - 부분 배낭 문제 (0) | 2021.11.28 |
| A010_FloydWarshall (0) | 2021.11.11 |
